According to a quick google search, the maximum volume of a grand piano in a small room is about 109 dB. I didn't come across detail, but I assume that's a huge multi-finger hit and not achievable on a single key, and I don't know how far from the sound board that measurement came from, but I thought it was an interesting tidbit. Not that keyboards should necessarily be limited to the dynamic range of a piano on one hand, nor, on the other hand, are most sound systems capable of actually reproducing the full dynamic range of what the human ear can hear before we go deaf (nor is there any need for most of us to attempt to duplicate the actual sound level of a gun shot, even if we had a sound system that was capable of it).burningbusch wrote:Musical instruments have no where near a 120db amplitude range.
Some other thoughts from this thread...
Your fingers are capable of an infinite number of different levels between zero and maximum, regardless of one's ability to replicate a given level at will, which is a red herring. The fact that we don't have perfect control doesn't mean our playing doesn't create audible differences. Humans have a certain amount of randomness to their motions, we can't be so precise, and that imprecision is part of the character of our playing. If you take out the ability of something to respond to deviations smaller that we can control, it will sound robotic.
The worst argument I saw was that the 8 levels of dynamics of a traditional score are sufficient. Can you just imagine how bad a piano patch would sound if every velocity level was rounded to one of the nearest 8? Ouch! Engineering down to our primitive ability to notationally score the tremendous range of what our fingers can do and what our ears can hear would be a bad idea indeed! And, btw, there is a traditional notation for many levels between those 8... crescendo and decrescendo. They do not mean you should attempt to jump through the 8 steps without anything in between!
If we accept that our ears can't recognize a difference of less than 1 dB, then 110 steps should be sufficient to duplicate a 109 dB piano. However, there are still areas where that can theoretically fall short. For one thing, there is rounding error. If 1000 "real" velocity values are each rounded to the closest of 100 values, some will round in such a way that an inaudible difference between two close notes will round to something that creates an audible difference. (That is, if the velocity that would create 50.4 db is rounded down to 50, and the velocity that would create 50.6 db is rounded up to 51, you have now created an audible 1 dB difference between the two notes that, on a real piano, would have been only an inaudible .2 dB apart.) Then, as already mentioned, there is the variable of scaling velocity curves... the resolution of differences in force is not linear, and resolution you add somewhere is lost somewhere else.
But I agree that this is largely academic. Velocity range or distinction between levels is not anything I ever considered a problem. In reality, we listen to music on devices with limited dynamic range to begin with, and the amount of level control we have, keeping in mind our 1 dB audible differentiation capability, really does seem perfectly adequate to me; whatever "errors" are introduced seem likely to be minimal. I agree with those that think that velocity curves can make a big difference in playability, though. The Kawai approach of being able to customize the response to your playing sounds like it could be a very useful feature.
Whether anyone has actually tried to create a velocity curve that would somehow correlate, I don't know.
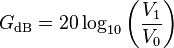(where V0 and V1 are the two values to be compared) - combined with psychoaoustical research the common consensus appears to be that a perceived doubling of volume happens at approximately 6 dB increase in sound pressure level. This would not imply that 1 dB is the smallest perceivable difference - and even if it would be established by any organisation I'd loudly protest against! 
No need to chime in.
](./images/smilies/eusa_wall.gif "Brick wall"){kind=small}